 1 2 3
1 2 3
Инструменты с фиксированным доходом (Fixed Income), самыми распространёнными из которых являются государственные облигации, значительно менее популярны у отечественных инвесторов (особенно мелких), чем корпоративные ценные бумаги. Тому есть несколько причин : невысокая (особенно в последние годы) доходность, ограниченный выбор инструментов как по срокам погашения, так и по другим характеристикам, недостаточная ликвидность по многим выпускам, более сложные, по сравнению с акциями, и не всегда понятные начинающему (и не только) инвестору методы расчёта основных показателей данного рынка, требующие к тому же определённых навыков в обращении с электронными таблицами (Excel). Несмотря на всё вышесказанное долговой рынок (ещё одно название рынка облигаций) представляет интерес для самых разных типов инвесторов : во-первых, как сегмент финансового рынка с минимальным риском и стабильной (хотя и невысокой) доходностью, служащей также индикатором т.н. "безрисковой" доходности ; во-вторых, как возможность диверсификации высокодоходного и рискованного портфеля корпоративных бумаг ; в-третьих, как средство урегулирования разнонаправленных потоков платежей (управление ликвидностью) и др.. Ниже в этом разделе будут рассмотрены основные показатели долгового рынка, методы их расчёта и интерпретации, а также базовые торговые стратегии, достаточные для начала осмысленной работы с инструментами с фиксированной доходностью.
Сам термин "облигация" (obligation), в переводе означающий "обязательство", представляет собой обязательство эмитента (т.е. субъекта рынка, выпустившего облигацию) выплатить на строго определённых условиях некоторую сумму(ы) владельцу облигации, а также произвести определённые действия (например, конвертировать облигации в акции). Определяющим для рынка облигаций является понятие доходности, которое, в свою очередь, опирается на концепцию временной стоимости потоков платежей. Суть этой концепции в разной стоимости денег во времени, и разница эта является платой за пользование деньгами и зависит от нескольких факторов : премии за риск, величины безрисковой ставки, ликвидности, срочности и др.. Соответственно, инвестор, вкладывая деньги в облигацию (т.е. предоставляя кредит эмитенту), рассчитывает (иногда, безосновательно J ) на получение адекватного вознаграждения от эмитента за пользование деньгами. Величина такого вознаграждения в процентах от суммы предоставленного кредита называется ставкой дохода (процента) и обычно обозначается r (rate, return).
r = (FV/PV – 1 )*100% , где
r —ставка дохода ;
PV (Present Value) — текущая(приведённая) стоимость денег ;
FV (Future Value) — будущая стоимость денег.
Вторым параметром, определяющим доходность, является срок, за который было получено вознаграждение. Таким образом, доходность можно определить как разность между текущей и будущей стоимостью инвестиции, полученную за определённый срок. Для того, чтобы можно было сравнивать доходности инвестиций с различными сроками и значениями ставок дохода, обычно используют годовую ставку процента (хотя можно использовать и месячную, и квартальную, и любую другую).
Существует два способа начисления процентов: по простой процентной ставке и по сложной . При использовании простой процентной ставки проценты начисляются только на первоначальную сумму инвестиций, тогда, как при использовании сложной процентной ставки проценты начисляются не только на начальную сумму, но и на уже начисленные проценты (т.е. происходит реинвестирование процентных выплат). Таким образом, при начислении дохода по простой процентной ставке начальные инвестиции со временем растут по линейному закону, а при использовании сложной процентной ставки – экспоненциально.
простые проценты:
FV=PV(1 + r*n) , где
n – число периодов начисления процентов.
сложные проценты:
FV=PV(1 + r) n , где
n – число периодов начисления процентов
Процесс определения будущей стоимости называется наращением, а коэффициент (1 + r) n называется коэффициентом наращения. Часто, при использовании сложных процентов и периода начисления меньше года (т.е. проценты начисляются несколько раз в году), применяются номинальная и эффективная процентные ставки. Номинальная процентная ставка – это объявленная каким-либо образом процентная ставка, равная произведению ставки дохода, используемой для начисления в каждом периоде, на количество периодов начисления процентов, а эффективная процентная ставка соответствует реальной сумме полученных инвестором платежей, отнесённых к инвестированной сумме и равна коэффициенту наращения для каждого периода, возведённому в степень, равную числу периодов начисления процентов. К примеру, банк, используя сложные проценты, начисляет каждый квартал 4% :
номинальная процентная ставка в этом случае равна : (0,04*4) = 16% годовых ;
эффективная процентная ставка в этом случае равна : (1+0,04)4 – 1 = 16,99% годовых.
Соотношение между эффективной и номинальной ставками процента:
rэф = (1 + rном /n) n – 1 ;
Для того, чтобы определить сегодняшнюю стоимость некоторой суммы, получаемой в будущем, используется процесс, обратный наращению. Процесс определения текущей стоимости будущего платежа (потоков платежей) называется дисконтированием,
простые проценты:
PV = FV /(1 + r*n) , где:
n – число периодов начисления процентов.
сложные проценты:
PV = FV /(1 + r) n , где
n – число периодов начисления процентов.
Каждый трейдер, торгующий облигациями, использует математические формулы для двух основных целей – определения стоимости ценных бумаг и количественной оценки риска своей открываемой(или открытой) позиции. Узловым моментом всех расчётов, связанных с облигациями, является взаимосвязь цены и доходности. Облигационные трейдеры и аналитики, рассматривая и обсуждая положение дел на рынке облигаций и давая рекомендации об открытии или закрытии позиций, оперируют, как правило, в терминах доходности. В то же время, реальные результаты работы трейдера (т.е. его прибыли и убытки) зависят от изменений цен на инструменты долгового рынка. Таким образом, трейдер, принимающий решение о покупке или продаже облигаций, вынужден решать две основные задачи : во-первых, спрогнозировать величину и направление изменения доходности ; во-вторых, преобразовать свой прогноз относительно изменения доходности в прогноз изменения цены и прибыли. Решение первой задачи достаточно субъективно и во многом зависит от представлений трейдера о текущей экономической ситуации, методов, используемых для прогнозирования кривой доходности, инвестиционных целей и ограничений по риску, особенностей налогообложения и т.д.. Для решения второй задачи большинство тредеров используют достаточно стандартные математические методы, позволяющие с высокой степенью точности вычислять значения цен и риска, соответствующие имеющемуся прогнозу. Далее в этом разделе мы сначала рассмотрим методы вычисления основных показателей долговых ценных бумаг (таких, как цена, доходность, дюрация, выпуклость), а затем, перейдём к анализу кривой доходности.
Обращающиеся на отечественном рынке облигации можно разделить на два основных типа – бескупонные(дисконтные) и купонные(процентные). К бескупонным облигациям (в финансовой литературе и на Западе их часто называют "zero-bond", т.е. облигации с нулевым купоном) относятся ГКО – государственные краткосрочные обязательства, выпускаемые (точнее, эмитируемые) Министерством Финансов РФ на срок менее года (что ясно из названия). Этот вид облигаций выпускается и обращается с дисконтом, так как единственный ожидаемый будущий денежный поток – это номинальная (выкупная) цена облигации в конце срока обращения. Доход образуется за счёт разницы между текущей стоимостью облигации в момент её приобретения и стоимостью в момент погашения или продажи. Поскольку будущая стоимость (цена погашения) для облигаций известна заранее – это номинал, то, как правило, требуется определить либо доходность к погашению для текущей цены, либо цену облигации для заданной или текущей доходности. Таким образом, доходность (доходность к погашению) ГКО рассчитывается по формуле:
Y = (FV/PV – 1)*(365 / t )*100% , где
t – срок до погашения облигации в днях ;
Формула для расчёта текущей стоимости (цены) облигации находится путём дисконтирования будущей стоимости (номинала) по существующей или прогнозируемой ставке доходности :
PV = FV /(1 + r*( t /365 )) , где
t – срок до погашения облигации в днях ;
Пример: трейдер имеет ГКО 21160 со сроком погашения 20.11.2002 и номиналом 1000рублей. Определим доходность к погашению, если текущая цена этой бумаги составляет 950 рублей и до погашения осталось 170 дней : (1000руб. / 950руб. – 1)*(365/170)*100% = 11.3% годовых ; Определим цену этой ГКО за два месяца до погашения (на 20 сентября) и при прогнозируемой доходности 12% годовых : 1000руб. / (1+0.12*(61/365)) = 980.34руб. ;
*Как мы увидим далее, определение стоимости облигации с нулевым купоном (т.е. дисконтирование будущего платежа по соответствующей ставке) – один из основных элементов в определении стоимости вообще всех облигаций.
Купонные облигации являются ценными бумагами, дающими своим владельцам право на периодическое получение процентного (купонного) дохода. При этом, здесь возможно также получение дисконта, если цена приобретения облигаций (при первичном размещении или на вторичных торгах) будет меньше цены их реализации, в том числе при погашении облигаций по их номиналу. К купонным облигациям относятся ОФЗ – облигации федерального займа, которые бывают ПД (постоянный купонный доход), т.е. размеры всех купонов определяются как постоянная величина на весь период до погашения,ФД (фиксированный купонный доход), т.е. величина купонного дохода устанавливается при выпуске как фиксированная величина, которая может различаться для различных периодов выплат и АД (амортизационный доход), т.е. погашение номинальной стоимости облигаций осуществляется по частям.
Наибольший интерес для трейдера среди купонных бумаг в настоящее время представляют (по моему мнению) ОФЗ-ФД. Они достаточно ликвидны, имеют высокую частоту выплаты купонов – поквартально, большой срок обращения – более 4 лет, большое количество выпусков. Поскольку по купонным бумагам периодически выплачивается проценты, их держатель получает право на серию процентных платежей и выплату основной (номинальной) суммы при погашении облигации. Каждый из этих платежей является обособленным денежным потоком, получаемым в определённый момент в будущем, поэтому отдельный платёж по своей сути не отличается от платежа по бескупонной облигации. Текущая стоимость такого денежного потока находится с помощью дисконтирования по соответствующей процентной ставке, т.е. купонную облигацию можно представить как портфель бескупонных облигаций с различными сроками погашения и номиналами. Каждый купон и выкупная цена индивидуально дисконтируется по определённой процентной ставке, причём для разных купонов она может быть разной. Затем, рассчитанные таким образом стоимости суммируются, и определяется текущая цена облигации. Формула для расчёта текущей стоимости (цены) ОФЗ при существующей или прогнозируемой ставке доходности r :
PV = ∑CF /(1 + r) t /365 + N /(1 + r) t /365 , где
t – срок до выплаты купона или погашения облигации в днях,
CF – купонный платёж ;
N – номинал облигации (выкупная сумма).
*Обратите внимание, что в вышеприведённой формуле для дисконтирования потока будущих платежей используется эффективная ставка доходности.
Итак, мы определили текущую цену интересующей нас облигации, но если Вы посмотрите на биржевые котировки данной бумаги, то, скорее всего, увидите другую цену, которая отличается от "нашей" в меньшую сторону. Дело в том, что биржевые котировки купонных облигаций на ММВБ (да, и на большинстве западных организованных рынков) отражают так называемую "чистую" цену, которая не включает в себя накопленный с момента выплаты последнего купона купонный доход, указываемый, как правило, отдельно в соответствующей колонке таблицы биржевых котировок. Несмотря на то, что купонный доход выплачивается эмитентом облигаций тому лицу, которому они принадлежат на дату погашения или выплаты купона, каждый предыдущий владелец также имеет право на получение дохода пропорционально сроку владения. Это достигается тем, что при приобретении облигаций их покупатель должен выплатить прежнему владельцу помимо "чистой" цены облигаций также и величину накопленного купонного дохода. Таким образом, вышеприведённая формула для расчёта текущей стоимости купонной облигации (PV) определяет "грязную" цену, т.е. реальную цену, которую придётся заплатить за облигацию, а для нахождения "чистой" цены необходимо вычесть из "грязной" цены сумму накопленного купонного дохода (A), которая рассчитывается следующим образом :
A = C( T – t ) / T , где:
T — длительность купонного периода (в днях);
t — количество дней, оставшихся до выплаты ближайшего купона;
C — размер ближайшего купона (руб.).
Надо также отметить, что обычно купоны объявляются в виде купонной ставки в процентах годовых и для того, чтобы рассчитать величину купонов, выплачиваемых несколько раз в году, необходимо применять следующую формулу :
C = r* (T /365)*N , где:
T — длительность купонного периода (в днях) ;
r — купонная ставка;
N — номинал облигации (руб.).
, т.е. в данном случае для определения размера купонного дохода используется номинальная ставка.
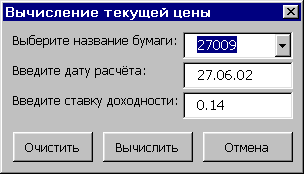
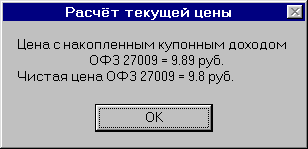
*Я использую для расчёта текущей стоимости (цены) ОФЗ программу, написанную мной на VBA (Visual Basic for Applications). В программу нужно лишь ввести название бумаги, дату, на которую необходимо вычислить цену и значение ставки доходности, по которой будет дисконтироваться поток платежей. С кодом программы можно ознакомиться в разделе "Торговые системы".
Ещё хочу обратить Ваше внимание на следующий момент – в вышеприведённых формулах для дисконтирования будущих потоков платежей используется одна ставка процента, т.е. неявно предполагается , что все получаемые в будущем суммы купонных выплат будут реинвестироваться под одинаковый и, к тому же, определяемый в текущий момент, процент. Такое предположение выглядит малореалистичным, т.к. не учитывает форму и другие свойства кривой доходности (подробнее об анализе кривой доходности читайте ниже). Тем не менее, такой подход получил широкое распространение и используется большим количеством трейдеров.
Доходность
Доходность к погашению купонных облигаций зависит от их цены, но алгебраическим путём невозможно определить доходность непосредственно из цены, поэтому доходность определяется из вышеприведённой формулы для расчёта текущей стоимости купонной облигации (PV) численными методами с помощью итерационных процедур. Для этого обычно используются методы решения нелинейных уравнений с применением итерационных процедур, такие как метод сканирования, метод Ньютона, метод хорд и т.п..
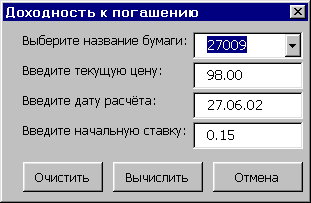
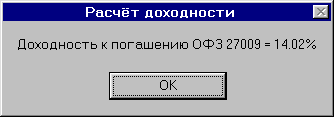
*Я использую для вычисления доходности к погашению ОФЗ программу, написанную мной на VBA (Visual Basic for Applications), в которой для определения доходности используется метод деления отрезка пополам. В программу нужно лишь ввести название бумаги, дату, на которую необходимо вычислить доходность, текущую "чистую" цену и и начальное значение ставки доходности (приближённое) для быстроты вычислений.С кодом программы можно ознакомиться в разделе "Торговые системы".
Надо заметить, что доходность к погашению не единственный вид доходности, используемый финансовыми аналитиками – существует несколько других разновидностей доходности, среди которых можно упомянуть текущую доходность, рассчитываемую по следующей формуле:
Ycur = (C /PV )*100%
Ycur = (((C + PVt+1)/PV )-1)*(365/t) *100% (мой вариант J)
Эта формула позволяет определить доходность к выплате ближайшего купона. Поскольку этот метод определения доходности предполагает неизменность "чистой" цены на конец расчётного периода по отношению к его началу, его использование имеет смысл только на короткий срок и в условиях низкой волатильности процентных ставок. Второй вариант данной формулы предусматривает реализацию облигации на следующий день после выплаты купона (t+1), для чего вычисляется приведённая стоимость облигации в этот момент, дисконтированная по заданной прогнозируемой процентной ставке. Этот метод позволяет более точно и реалистично определять доходность к ближайшей выплате.
Вот несколько основных правил, описывающих соотношение цены и доходности купонных облигаций :
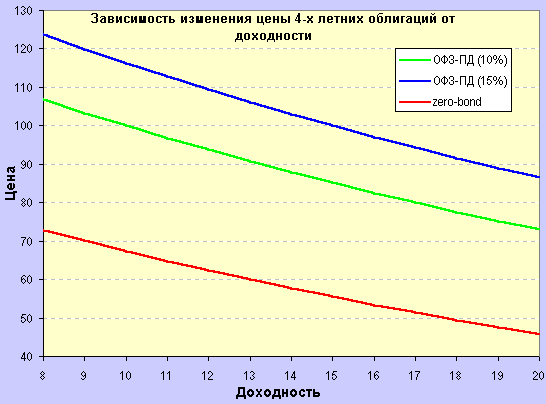
Рис.1