1 2 3
1 2 3
Дюрация и выпуклость
Как я уже говорил выше, каждый трейдер, торгующий облигациями, использует математические формулы для двух основных целей – определения стоимости ценных бумаг и количественной оценки риска своей открываемой (или открытой) позиции. Основные методы определения стоимости облигаций были нами рассмотрены, но они не позволяют оценить напрямую степень риска, которому подвергается позиция в случае изменения доходности. Для этой цели используется такое понятие как дюрация (duration - длительность) – величина, зависящая от срока до погашения облигации и величины купонных выплат, которая количественно связывает колебания рыночного курса облигации с колебаниями рыночной процентной ставки. Это понятие ввёл Фред Маколи (Macaulay F.R.), чтобы получить лучшую, чем срок до погашения, оценку продолжительности инвестирования в облигацию и, таким образом, оценку риска по прибыли для держателя облигации, поскольку, портфельные менеджеры давно поняли, что риск держателя облигации не пропорционален сроку до погашения, т.к. платежи в отдалённом будущем в меньшей степени учитываются в цене, чем ближайшие выплаты. Маколи определил дюрацию как средневзвешенный по приведённой стоимости срок до погашения всех платежей по облигации. Дюрация имеет размерность времени, т. е. выражается в годах. Учитывая, что бескупонные облигации имеют только один платёж – в момент погашения, равный номиналу, дюрация для них всегда равна сроку до погашения.
D = å (tnx CFn) / (1 + r)t n/ å CFn / (1 + r)t n , где
t – срок до выплаты купона или погашения облигации в годах,
CF – платёж ;
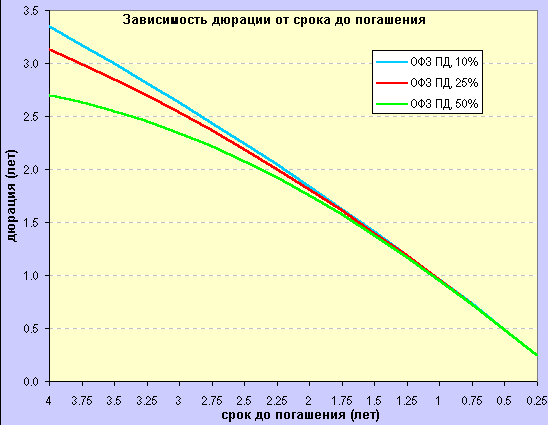
Рис.2
Обычно для лучшего понимания сути дюрации приводят набивший всем оскомину пример с банками с водой, предложенный выдумщиками из Salomon Brothers, но я этого делать не стану J , поскольку для нас более важным свойством дюрации является то, что она показывает величину изменения цены в ответ на единицу изменения доходности (обычно – 1%), что, в свою очередь, позволяет нам, наконец-то, количественно измерить риск своей открываемой (или открытой) позиции. На Западе этот показатель называют также ценовой риск (или долларовая дюрация), т.к. он показывает, на сколько долларов(или других денежных единиц) изменится цена облигации при изменении доходности на 1%.
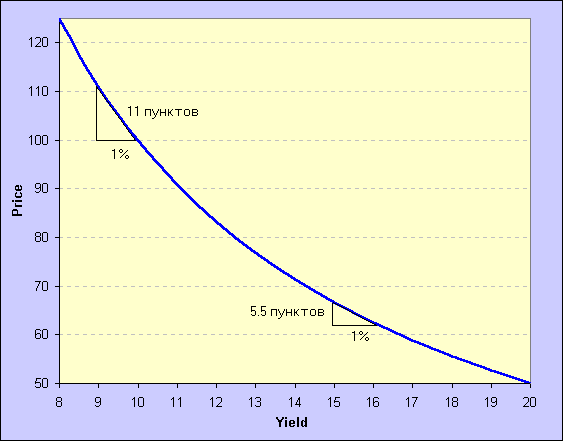
рис.3
Рисунок 3 иллюстрирует скорость изменения цены по отношению к изменению доходности как функцию доходности облигации. Два выделенных отрезка – касательные к кривой цена-доходность в точках со значениями доходности 9% и 15%. Каждый из этих касательных отрезков соответствует 1%-му изменению доходности вдоль оси Х. Обратите внимание на разные углы наклона этих касательных. Это показывает, что величина изменения цены для заданного изменения доходности зависит от уровня доходности. Изменение доходности с 9 до 10% приводит к понижению цены на 11 пунктов, тогда как изменение доходности с 15 до 16% вызывает уменьшение цены только на 5.5 пунктов. Сответственно, в первом случае долларовая дюрация будет равна 11 центам (будем считать один пункт равным одному центу), а во втором случае – 5.5 центам. Таким образом, для малых изменений доходности дюрация приближённо равна :
D = – D P / DY , где :
P – полная ("грязная") цена облигации ;
Y – доходность облигации ;
D – изменение цены или доходности облигации.
Знак "минус" присутствует в формуле потому, что доходность и цена всегда изменяются в противоположных направлениях.
Поскольку наклон касательной к непрерывной кривой равен частной производной функции, описывающей кривую, точное значение дюрации равно :
D = – ¶ P / ¶ Y , где :
P – полная ("грязная") цена облигации ;
Y – доходность облигации ;
¶ – производная.
Учитывая, что текущая цена облигации, как правило, отлична от номинала, а инвестор рассчитывает величину риска по отношению к объёму инвестированных средств, более практично использовать показатель модифицированной дюрации, отражающий процентное (относительно текущей цены) изменение цены облигации при изменении доходности.
MD = (– ¶ P / ¶ Y) / P *100%
В вышеприведённом примере при долларовой дюрации, равной 11 центам, модифицированная дюрация составит 9.91%, а при снижении долларовой дюрации до 5.5 центов (т.е. в два раза) модифицированная дюрация снизится до 8.21% (т.е. только на 17%). Это происходит потому, что цена облигации падает с ростом доходности. Вообще, модифицированная дюрация ближе к линейной функции, чем долларовая, т.к. учитывает изменения в цене облигации. В дальнейшем, употребляя термин "дюрация", я буду иметь в виду модифицированную дюрацию.
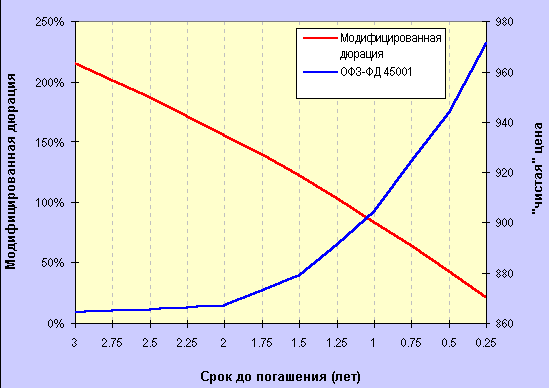
Рис.4
Поскольку кривая цена-доходность выпукла (что означает, что её наклон непрерывно меняется) и имеет отрицательный наклон (который, как уже было сказано, и является дюрацией, взятой со знаком "минус")), расчёт изменения цены облигации с помощью показателя дюрации будет не точным (будучи линейным приближением, изменение цены будет приблизительно равно движению вдоль касательной, т.е. прямой, а не кривой), преувеличивая возможное снижение цены и преуменьшая рост.
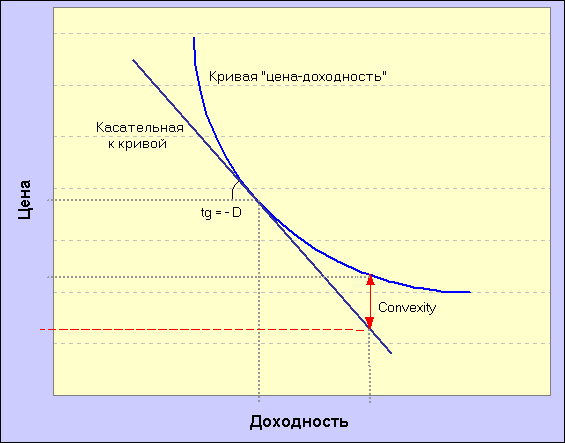
Рис.5
Для повышения точности вычисления изменения цены в зависимости от изменения доходности используется ещё один важный показатель рынка долговых бумаг, называемый выпуклостью (convexity, Cx), являющийся квадратичным приближением. Выпуклость характеризует скорость изменения наклона кривой цена-доходность и представляет собой вторую производную цены облигации по доходности :
Cx = 1/2*(¶ 2P / ¶ Y2) / P , где :
P – полная ("грязная") цена облигации ;
Y – доходность облигации ;
Выпуклость всегда положительна.Чем больше скорость изменения, тем больше меняется дюрация при изменении доходности.Таким образом, если дюрация – это скорость изменения цены облигации при изменении доходности, то выпуклость – это ускорение.
Используя разложение рядов Тейлора для аппроксимации будущей цены облигации получаем следующий алгоритм вычислений :
Pf = P + h*( ¶ P / ¶ Y) + h2 * (¶ 2P / ¶ Y2) *1/2 , где :
Pf – цена облигации после изменения ставки ;
P – текущая ("грязная") цена облигации ;
Y – доходность облигации ;
h – величина изменения ставки в десятичном формате.
Пример: рассчитаем, используя разложение рядов Тейлора, цену ОФЗ-ФД 27013 по состоянию на 15 августа 2002 года в случае изменения текущей доходности к погашению (ставки дисконтирования) с 14% до 15% годовых. Полная ("грязная") цена будет равна 1012.19 руб., первая производная цены по доходности равна – 1413.68, вторая производная цены по доходности равна 3390.91, величина изменения ставки в десятичном формате составит 0.01.
Pf = 1012.19 руб. + 0.01* – 1413.68 + 0.012 * 3390.91 * 1/2 = 1012.19 руб. – 13.97 руб. = 998.22 руб.
Такой же результат даёт использование непосредственно модифицированной дюрации и выпуклости :
Pf = P + h*(MD + Cx ) , где :
Pf – цена облигации после изменения ставки ;
P – текущая ("грязная") цена облигации ;
MD – модифицированная дюрация ;
Cx – выпуклость ;
h – величина изменения ставки в десятичном формате.
Pf = 1012.19 руб. + 0.01* (– 139.665% + 1.675%) = 1012.19 руб. – 1.38 % = 998.22 руб.
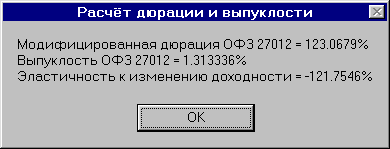
*Для расчёта модифицированной дюрации, выпуклости и общей чувствительности (эластичности) облигации к изменению доходности я использую программу, написанную на VBA (Visual Basic for Applications). В программу нужно лишь ввести название бумаги, дату, на которую необходимо вычислить дюрацию и выпуклость и значение ставки доходности.С кодом программы можно ознакомиться в разделе "Торговые системы".