 1 2 3
1 2 3
Этап шестой. Определить эффективное множество. Одним из основных постулатов теории Марковица является утверждение о том, что при выборе портфеля инвестор должен опираться при принятии своего решения исключительно на ожидаемую доходность и риск (СКО), основываясь на соотношении этих двух параметров и своём отношении к риску и доходности, отражаемом так называемыми "кривыми безразличия". Эти кривые могут быть представлены в виде двухмерного графика, где по горизонтальной оси отложен риск, а по вертикальной оси – доходность. Следующие рисунки демонстрируют кривые безразличия инвестора, не расположенного к риску и, соответственно, рискованного инвестора.
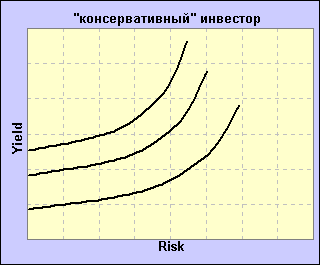
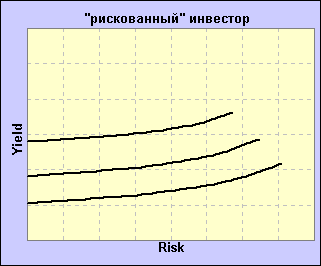
Данные кривые могут служить наглядной иллюстрацией отношения различных типов инвесторов к соотношению риска и доходности вообще, и к маржинальной торговле в частности. "Консервативный" инвестор вряд ли будет использовать в своей торговле "плечо", т.к. по мере роста риска инвестиций требуемое им вознаграждение возрастает непропорционально, т.е. значительно сильнее, в то время как использование маржи (заёмных средств) приводит к пропорциональному возрастаниию риска и доходности. Концепция кривых безразличия опирается на два основных предположения : во-первых, предполагается, что инвестор, выбирая между двумя или более идентичными во всём, кроме ожидаемой доходности, портфелями, предпочтёт портфель с большей ожидаемой доходностью ; во-вторых, предполагается, что инвестор, выбирая между двумя или более идентичными во всём, кроме ожидаемого риска, портфелями, предпочтёт портфель с меньшим ожидаемым риском. Эти предположения легли в основу т.н. теоремы об эффективном множестве, которая гласит :
Инвестор выберет свой оптимальный портфель из множества порфелей, каждый из которых :
Теперь давайте вернёмся к полученному нами на предыдущем этапе множеству допустимых портфелей и, применяя теорему об эффективном множестве, определим его (эффективного множества) местоположение.
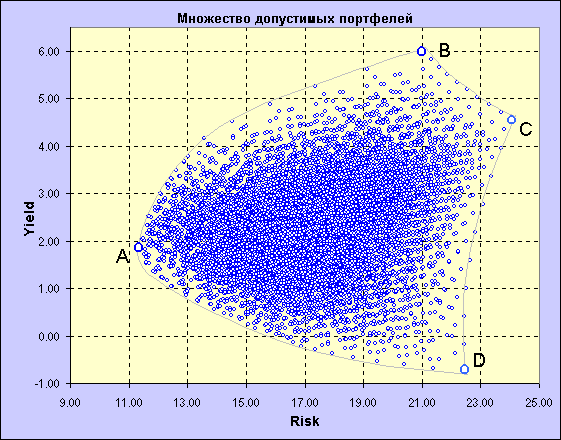
Сначала выделим множество портфелей, удовлетворяющих первому условию теоремы. Если посмотреть на рисунок, можно заметить, что портфель А обладает минимальным риском из всех допустимых портфелей. При этом не существует более рискового портфеля, чем портфель С. Таким образом, множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы множества допустимых портфелей, расположенная между точками А и С. Теперь выделим множество портфелей, удовлетворяющих второму условию теоремы об эффективном множестве. Самым доходным среди достижимого множества является портфель В, а портфелем, обеспечивающим наименьшую ожидаемую доходность, является портфель D. Следовательно, множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества, расположенная между точками D и В. Учитывая, что оба условия теоремы об эффективном множестве должны выполняться одновременно, искомым эффективным множеством будет пересечение двух вышеописанных множеств, располагающееся на верхней левой границе множества допустимых портфелей между портфелями А и В. Портфели, составляющие эту границу, называются "эффективными", а сама граница часто именуется "эффективным фронтом".
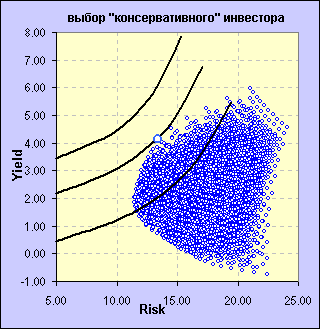
Из этого множества эффективных портфелей инвестор выбирает оптимальный для себя портфель, руководствуясь своим отношением к риску и доходности. Для этого инвестору надо на графике, содержащем эффективное множество, нарисовать свои кривые безразличия и выбрать портфель, расположенный на кривой безразличия, находящейся выше и левее остальных (что вытекает из важного свойства кривых безразличия : инвестор будет считать более привлекательным любой портфель, лежащий на кривой безразличия, находящейся выше и левее). Этот портфель будет соответствовать точке касания кривой безразличия и эффективного множества.
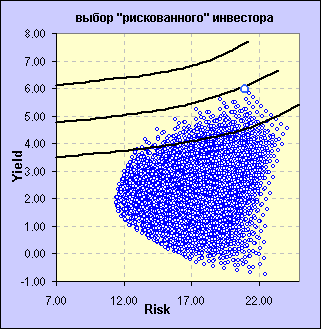
Для вычисления непосредственно эффективных портфелей в виде самостоятельного ряда данных могут быть использованы различные вычислительные процедуры и методы, используемые для решения оптимизационных задач : интегрирование с применением множителей Лагранжа, метод "критических линий", предложенный самим Марковицем (также известный как метод "угловых портфелей"), симплексный метод и др.. Используя свойство эффективности портфеля, означающее, что любой другой портфель имеет либо больший риск, либо меньшую доходность, я написал небольшую программу на VBA, в основе алгоритма которой лежит симплексный метод, позволяющую вычислить непосредственно эффективные портфели. На рисунке ниже изображены эффективные портфели, соответствующие обоим представленным выше достижимым множествам – как с ограничением минимального объёма средств, инвестируемых в каждую бумагу, так и без оного. "Звёздочкой" на рисунке отмечена точка с параметрами доходности ириска, соответствующими индексу РТС.
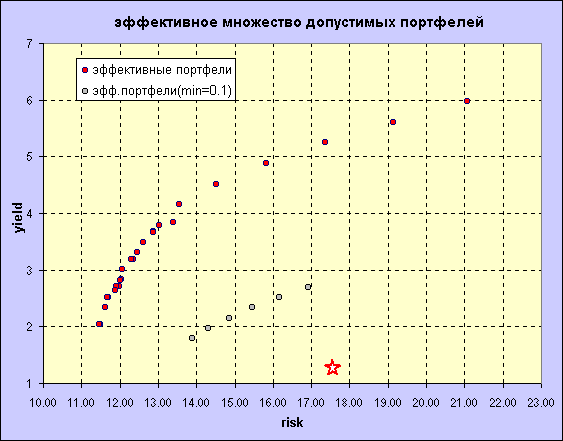
Данная гистограмма отображает структуру эффективных портфелей в зависимости от доходности и риска.
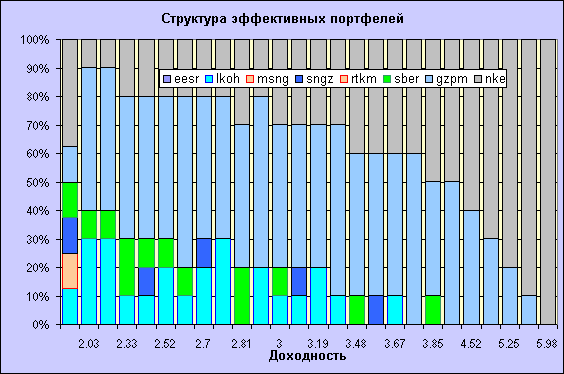
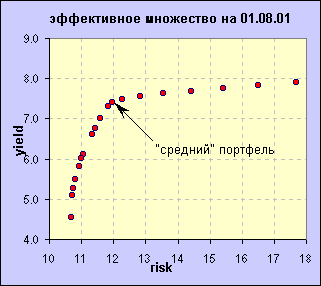
Итак, мы получили 26 эффективных (т.е. неулучшаемых) портфелей. Встанем на позицию осторожного, не расположенного к риску инвестора и выберем портфель с наименьшим риском и, соответственно, наименьшей доходностью. Сравним результаты нашего низкорискованного портфеля с результатами индекса РТС за первые два месяца 2001 года (напомню, что в качестве ожидаемой доходности мы использовали помесячные относительные изменения цен закрытия, неявно предполагая месячный горизонт инвестирования).
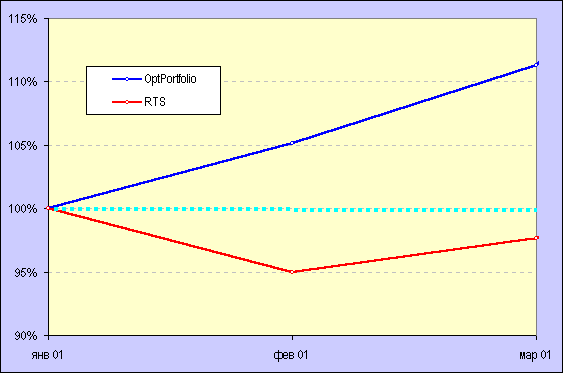
Результат, как видите, вполне может быть признан положительным. Тогда, как доходность индекса РТС составила за февраль –5%, доходность "оптимального" портфеля составила +5%, к концу марта доходность "оптимального" портфеля с начала тестового периода составляла уже +12%, в то время как доходность индекса РТС составила лишь –2%.
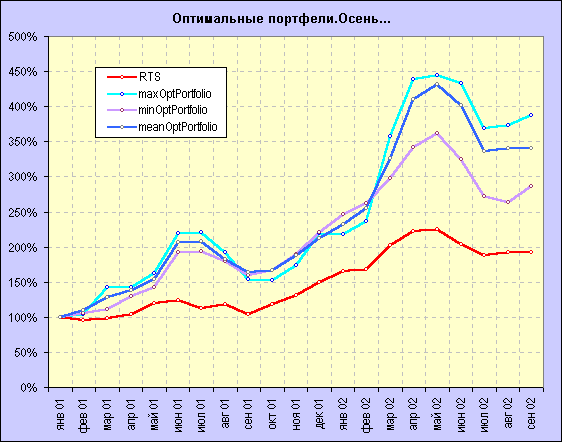
Для демонстрации финансовых результатов формирования оптимального портфеля ценных бумаг по методу Марковица на более длительном периоде времени, я провёл тестирование данного метода на исторических данных, начиная с 01.01.2001года и заканчивая 01.10.2002 года, с условиями и ограничениями, аналогичными использованным в нашем примере. Формирование (а, точнее, рЕформирование) портфеля производилось по окончании каждого месяца по методике, описанной выше. Из получаемого эффективного множества допустимых портфелей каждый раз отбирались три оптимальных портфеля, соответствующие портфелям с минимальным риском (условное название "minOptPortfolio"), с максимальной доходностью ("maxOptPortfolio") и, так сказать, "средний" портфель ("meanOptPortfolio"). Если с первыми двумя всё ясно, то критерии отбора третьего портфеля требуют некоторых пояснений. В том случае, если кривая "эффективного фронта" имела примерно равный наклон по всей длине, выбирался просто средний по значениям доходности и риска портфель. Если же начальный участок кривой "эффективного фронта" имел заметно больший угол наклона, нежели остальная её часть, то выбирался портфель, расположенный вблизи "точки перелома".
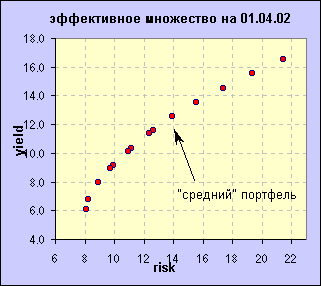
Глядя на график сравнительной динамики индекса РТС и вышеназванных оптимальных портфелей и учитывая довольно примитивный способ прогнозирования доходности и риска можно признать метод формирования оптимального портфеля ценных бумаг по Марковицу вполне работоспособным. Напомню, что в среде управляющих активами хорошим результатом считается достижение доходностиболее высокой, чем у "эталонного" индекса, т.н. "активной" доходности. В ходе проведённого тестирования удалось получить не только более высокую доходность, но и обойтись при этом значительно меньшим количеством бумаг (от 2 до 6), по сравнению с количеством, используемым при расчёте индекса РТС J, что делает задачу управления портфелем легковыполнимой и низкозатратной (низкий оборот, высокая ликвидность, упрощённый анализ и т.д.).
Задача определения кривой эффективного множества Марковица может быть сильно упрощена с помощью введения прцесса формирования дохода. Процессом формирования дохода называется статистическая модель, описывающая, как образуется доход по ценной бумаге. Рыночная модель Шарпа, являющаяся одной из таких моделей, относится к факторным, а точнее, однофакторным моделям, где в качестве фактора выступает доходность рыночного индекса. В частности, это предполагает, что изменение доходности отдельных ценных бумаг зависит от изменения доходности рыночного индекса (фактора) и связано с ним следующим образом :
ri = αiI + βiI rI + εiI , где :
ri – доходность ценной бумаги i за данный период ;
rI – доходность рыночного индекса I за данный период ;
αiI – коэффициент смещения ;
βiI – коэффициент наклона ;
εiI – случайная погрешность.
Как видите – простая линейная регрессия. Трудно, конечно, предположить, что такой сложный и многогранный процесс, каким является ценообразование на фондовом рынке, может быть полноценно описан при помощи столь простой линейной зависимости, однако, во-первых, данный подход лежит в основе многих более сложных и распространённых однофакторных и многофакторных моделей, таких как CAPM (модель оценки финансовых активов), APM (модель арбитражного ценообразования), BARRA и других, а во-вторых, однофакторная модель Шарпа, несмотря на присущие ей недостатки, широко используется при формирования портфеля ценных бумаг многими инвесторами. Таким образом, знакомство с ней необходимо и полезно J . Рассмотрим более подробно коэффициенты данного уравнения. Для наглядности будем использовать рисунок, изображающий график рыночной модели для ценной бумаги i в системе координат, где по вертикальной оси отложена доходность ценной бумаги i (ri), а по горизонтальной оси отложена доходность индекса I (rI).
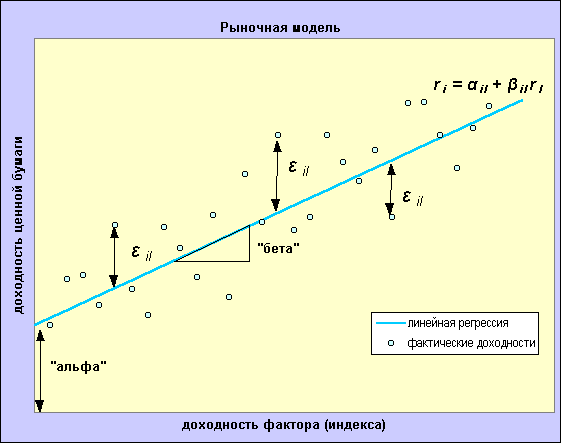
a ("альфа") – коэффициент вертикального смещения, некая константа, точка пересечения линии регрессии с вертикальной осью координат. С точки зрения финансового результата это означает либо регулярный прирост (при положительной "альфе"), либо регулярное снижение (при отрицательной "альфе") стоимости инструмента на некоторую постоянную величину. Знак и величина коэффициента "альфа" определяются либо выплатами, периодически производимыми по данному финансовому инструменту(дивиденды, купоны и т.д.), либо переоцененностью / недооцененностью инструмента участниками рынка, связанной с какими-то значимыми и продолжительно воздействующими факторами или событиями (ожиданием снижения мировых цен на нефть, грядущими реформами в отрасли и т.п.).Также, можно рассматривать альфа-коэффициент как отражение интереса участников рынка к активу – положительная "альфа" отражает повышенный интерес трейдеров к данному активу, отрицательная "альфа" свидетельствует о низком интересе (спросе).
Методом, чаще других используемым для нахождения параметров уравнения регрессии, является метод наименьших квадратов (МНК). Суть этого метода в нахождении линии, минимизирующей сумму квадратов значений ошибок (погрешностей) между величинами, рассчитанными по уравнению прямой, и фактическими значениями (в данном случае, доходностей). Величина "альфа"-коэффициента, в соответствии с этим методом, находится по следующей формуле :
αiI = ravg - βiI Ravg , где:
ravg – средняя доходность ценной бумаги i за данный период ;
Ravg – средняя доходность рыночного индекса I за данный период ;
βiI – коэффициент наклона.