 1 2 3
1 2 3
b ("бета") – коэффициент регрессии, отражающий наклон линии, вдоль которой рассеяны значения фактических доходностей ценной бумаги i. Наклон в рыночной модели ценной бумаги i измеряет чувствительность изменения её доходности к изменению доходности на рыночный индекс. Он может быть истолкован как показатель, характеризующий процентное изменение доходности ценной бумаги i, вызванное изменением доходности индекса рынка на единицу. "Бета"-коэффициент, кстати, является своеобразным аналогом модифицируемой дюрации, применяемой на рынке инструментов с фиксированным доходом, только там в качестве фактора выступает стихийно сложившаяся рыночная доходность на данном участке кривой доходности.
Величина "бета", минимизирующая суммы квадратов погрешностей, находится следующим образом :
βiI = σiI / σ2I, где :
σiI - ковариация между доходностью ценной бумаги i и доходностью индекса рынка ;
σ2I – дисперсия доходности рыночного индекса I.
Если величина коэффициента "бета" для некоторой бумаги больше 1, то это означает, что при изменении значения индекса рынка цена данной бумаги изменится в большей степени и в том же направлении. Если величина коэффициента "бета" меньше 1, но больше 0, то изменение индекса приводит к меньшему (по сравнению с индексом) изменению цены данной бумаги. Если же величина коэффициента "бета" меньше 0, то стоимость данной ценной бумаги изменяется в сторону, противоположную изменению значения рыночного индекса, что позволяет использовать данный финансовый инструмент для сокращения общего риска портфеля.
"Бета"-коэффициент наиболее широко применяется в инвестиционном анализе и менеджменте, являясь показателем того, насколько инструмент более (или менее) рискован, чем индекс.
ε – случайная погрешность (ошибка модели), отражающая тот факт, что обычно доходность ценной бумаги будет неточно описываться лишь движением индекса рынка, поскольку присутствуют и другие факторы, не включённые в рыночную модель. Разность между действительным и ожидаемым значениями доходности ценной бумаги при известной доходности рыночного индекса приписывается случайной погрешности. Значения случайной погрешности нормально распределены со средней, равной нулю, и постоянной дисперсией и рассчитываются следующим образом :
εiI = ri - (αiI + βiI rI ), где :
ri – действительная (фактическая) доходность ценной бумаги i ;
rI – доходность рыночного индекса I .
Исходя из рыночной модели, общий риск ценной бумаги i, измеряемый её дисперсией (или СКО), состоит из двух частей : рыночного (систематического) риска и собственного (несистематического) риска и вычислется по следующей формуле:
σ2i = β2iI σ2I + σ2εi , где :
β2iI σ2I – рыночный риск ценной бумаги i ;
σ2εi – собственный риск ценной бумаги i , мерой которого является дисперсия случайной погрешности.
Теперь, после ознакомления с основными принципами и допущениями рыночной модели, можно перейти к рассмотрению особенностей формирования эффективного множества допустимых портфелей по методу Шарпа.
Во-первых, рассчитаем по вышеприведённым формулам основные параметры рыночной модели для каждой ценной бумаги, включаемой в портфель. Для этого сначала вычисляется коэффициент "бета" :
| финансовый актив | EESR | LKOH | MSNG | SNGZ | RTKM | SBER | GAZP | NKEL |
|---|---|---|---|---|---|---|---|---|
| "Бета" | 1.19 | 0.973 | 1.004 | 0.925 | 1.062 | 0.667 | 0.144 | 0.9 |
затем – коэффициент "альфа" :
| финансовый актив | EESR | LKOH | MSNG | SNGZ | RTKM | SBER | GAZP | NKEL |
|---|---|---|---|---|---|---|---|---|
| "Альфа" | 3 | 0.041 | 1.149 | -0.02 | -2.76 | -1.51 | 2.159 | 4.922 |
и, наконец, вычисляется дисперсия (в нашем случае – СКО) случайной погрешности :
| финансовый актив | EESR | LKOH | MSNG | SNGZ | RTKM | SBER | GAZP | NKEL |
|---|---|---|---|---|---|---|---|---|
| СКО погрешности | 14.7 | 7.007 | 14.8 | 7.401 | 14.99 | 13.72 | 15.92 | 15.19 |
Теперь мы можем рассчитать доходность любого допустимого портфеля, определяемую как взвешенная сумма доходностей всех типов активов, входящих в портфель, по формуле :
Rp = å Wi (αiI + βiI rI + εiI), где :
Wi - относительный вес отдельногоактива в портфеле.
Общий риск портфеля, таким образом, равен :
σ2p = β2pI σ2I + σ2εp или σp = βpI σI + σεp , где :
βpI – коэффициент "бета" портфеля, вычисляемый как, соответственно, взвешенная сумма "бет" всех активов, входящих в портфель ;
σI – СКО доходности рыночного индекса ;
σεp – СКО случайной погрешности.
Данное уравнение показывает, что общий риск портфеля состоит из тех же двух компонентов, что и общий риск отдельных бумаг, т.е. – из рыночного и собственного риска. Таким образом, диверсификация (распределение капитала среди нескольких активов) может привести к снижению общего риска портфеля за счёт уменьшения собственного риска. Поскольку собственный риск портфеля определяется дисперсией (или СКО) случайной погрешности, то с увеличением количества включаемых в портфель бумаг ошибки модели – в силу случайного характера и предположения о некоррелированности отклонений доходности – будут взаимопогашаться, тогда как рыночный риск портфеля, определяемый произведением "беты" и дисперсии рыночного индекса, будет усредняться и стремиться к риску индекса рынка. Рисунок ниже иллюстрирует уменьшение общего риска портфеля в связи с увеличением количества включаемых в него ценных бумаг.
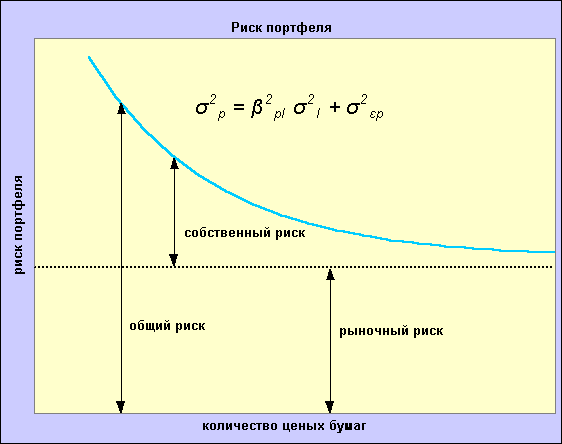
Также надо отметить ещё одно свойство составляющих общего риска портфеля, связнное с ожидаемыми доходностями. Поскольку рыночный риск связан с коэффициентом "бета" конкретной бумаги, при больших значениях "беты" значение рыночного риска (а значит и ожидаемая доходность) будет больше. Собственный же риск не связан с "бетой", поэтому увеличение собственного риска не ведёт к росту ожидаемой доходности. Таким образом, инвесторы вознаграждаются за принятие рыночного риска, тогда как собственный риск не компенсируется.
Вернёмся к эффективному множеству. Вот как выглядит множество допустимых портфелей при использовании для его расчёта рыночной модели. Для вычисления я использовал уже упоминавшуюся ранее программу, написанную на VBA, с параметрами и ограничениями, аналогичными тем, которые применялись при расчёте по методу Марковица.
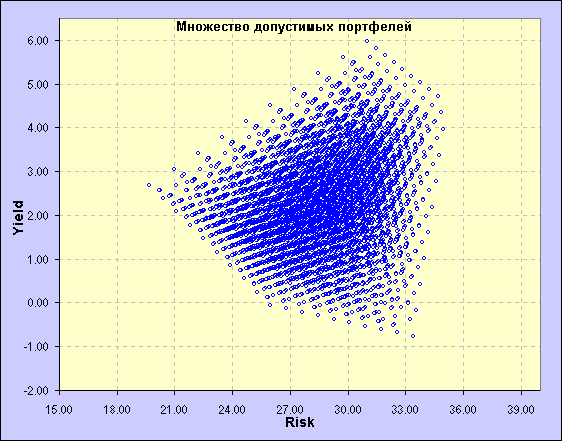
Прямолинейность границ данного множества определяется линейной функцией, используемой при расчёте параметров портфелей, в отличии от квадратичной функции, применяемой для расчёта риска в модели Марковица.
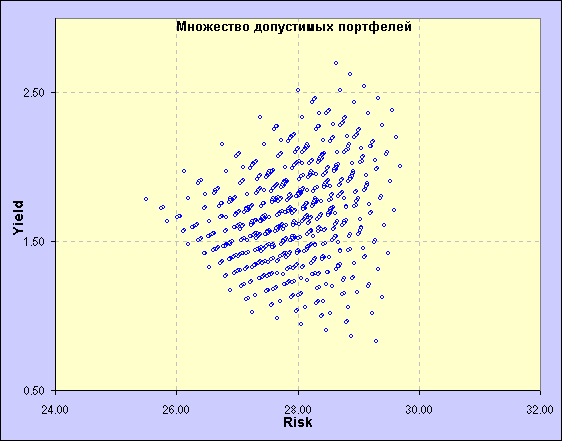
А вот так выглядят эффективные фронты при наличии ограничений на минимальный размер капитала, инвестируемого в каждую бумагу и без оного.
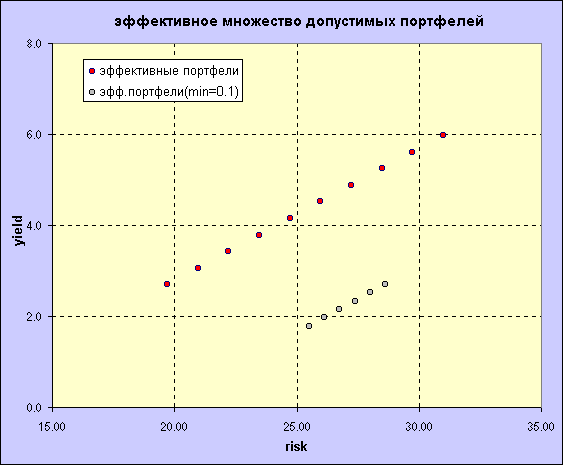
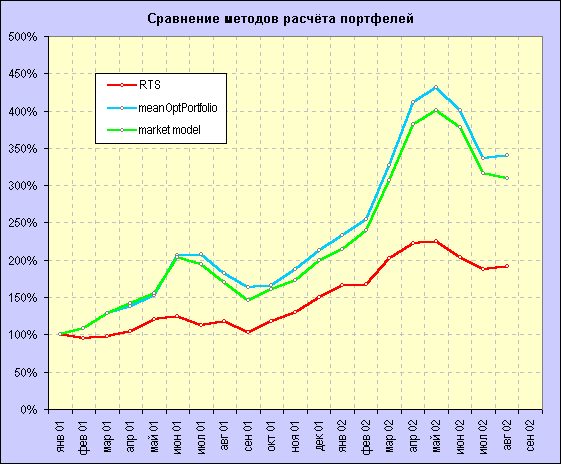
Проведя тестирование на исторических данных при условии ежемесячной "перетряски" портфеля я получил результаты, схожие с теми, которые были получены с использованием метода Марковица. Для сравнения использовались т.н. "средние портфели".
При использования рыночной модели важно оценить степень зависимости анализируемых инструментов от индекса. При низкой степени линейной зависимости значения "бета"-коэффициентов будут близки к нулю и получаемые оценки риска, соответственно, будут низкими, в то время, как риск, не связанный с индексом, может быть значителен и носить систематический характер. В то же время, низкие значения коэффициента "бета" не всегда свидетельствуют об отсутствии сильной линейной связи между индексом и инструментом – инструмент действительно может быть малорискованным J. Для оценки степени соответствия линии регрессии можно использовать коэффициент детерминации (R2). Для этого нам нужно рассчитать общую сумму квадратов отклонений (ОСК) и сумму квадратов отклонений, объясняемую регрессией (СКР). ОСК – это сумма квадратов разностей между фактической доходностью ценной бумаги и средней доходностью за расчётный период:
ОСК = å (ri - ravg )2, где :
ri - действительная (фактическая) доходность ценной бумаги i ;
ravg - средняя доходность ценной бумаги i .
СКР – это сумма квадратов разностей между прогнозируемой (рассчитанной в соответствии с рыночной моделью) доходностью ценной бумаги и средней доходностью за расчётный период:
СКР = å (ři - ravg )2, где :
ři - прогнозная величина доходности ценной бумаги i , вычисляемая, соответственно, по формуле рыночной модели (αiI + βiI rI ) ;
ravg - средняя доходность ценной бумаги i .
Таким образом, коффициент детерминации представляет собой отношение суммы квадратов отклонений, объясняемых регрессией (СКР), к общей сумме квадратов отклонений (ОСК) и даёт пропорцию изменения доходности ценной бумаги, объясняемую изменением доходности рыночного индекса :
R2 = СКР /ОСК =å(ři - ravg)2 / å(ri - ravg )2 .
Коффициент детерминации может принимать значения от нуля (когда доходность рыночного индекса не влияет на доходность ценной бумаги) до единицы (когда изменения доходности ценной бумаги полностью объясняются изменением доходности индекса рынка). Часто для наглядности значение коффициента детерминации умножается на 100%, при этом, чем значение R2 ближе к 100%, тем сильнее линейная связь индекса и ценной бумаги и, соотвественно, выше эффективность применения рыночной модели и – наоборот. Ниже представлены коффициенты детерминации, демонстрирующие степень связи месячных изменений индкса РТС и бумаг, используемых в нашем примере, на февраль 2001года, сентябрь 2001 года и август 2002 года (т.е. на период тестирования).
| финансовый актив | EESR | LKOH | MSNG | SNGZ | RTKM | SBER | GAZP | NKEL |
|---|---|---|---|---|---|---|---|---|
| "R2" | 67% | 86% | 59% | 83% | 61% | 42% | 2% | 52% |
| "R2" | 82% | 81% | 78% | 84% | 87% | 40% | 14% | 47% |
| "R2" | 46% | 78% | 69% | 78% | 45% | 78% | 28% | 51% |
Можно заметить, что изменения доходностей таких финансовых активов как Лукойл (об.) и Сургутнефтегаз (об.) на протяжении всего рассматриваемого периода в значительной степени связаны с изменением доходности индекса РТС, в то же время акции Газпрома демонстрируют практически полное отсутствие (на начало тестового периода) или незначительный "вклад" (на конец тестового периода) индекса РТС в дело изменения доходности данного актива. Тому есть несколько причин : во-первых, акции Газпрома не торгуются в Российской Торговой Системе и, соответственно, не включены в базу расчёта одноимённого индекса, что, в свою очередь, исключает непосредственное влияние изменения котировок акций Газпрома на значение индекса, во-вторых, в силу известных ограничений, связанных с торговлей акциями Газпрома на МФБ и процедурой перехода прав собственности, ценообразование этих акций трудно было назвать рыночным, поскольку оно в значительной степени контролировалось несколькими крупными игроками и т.д.
Итак, мы рассмотрели два базовых метода формирования портфеля ценных бумаг, являющихся основой для большинства применяемых ныне подходов. Конечно, существуют и другие способы формирования портфеля активов – многие управляющие используют для отбора бумаг фундаментальный анализ* (в этом случае применяются, как правило, различные виды метода капитализации доходов – модели дисконтирования дивидендов, к примеру, – и/или анализ удельных коэффициентов, характеризующих инвестиционную привлекательность отдельных предприятий или отраслей экономики, таких как P/E, EPS и т.п., непосредственно или с помщью моделей, подобных модели Грэхэма-Ри) или технический анализ* (в этом случае применяются, как правило, различные виды графических моделей и/или сигналы индикаторов и механических торговых систем, применяемых как к отдельным бумагам, так и к индексу рынка или отрасли). Иногда используются смешанные подходы к формированию портфеля : на этапе первичного отбора активов ("очерчивания рынка") применяются методы фундаментального анализа, а стоимостная структура портфеля определяется с помощью метода Марковица. В конечном итоге, выбор способов формирования портфеля ценных бумаг определяется инвестиционными предпочтениями конкретного управляющего активами или инвестора.
*Более детально фундаментальный и технический анализ рассмотрены в разделе "Акции".
В заключение хочу напомнить, что процесс портфельного инвестирования включает, кроме всего прочего, очень важный этап оценки эффективности управления портфелем ценных бумаг, но об этом - в следующем материале.
***
На этом, пока, всё … Любые замечания, поправки и предложения, как всегда, приветствуются.