 1 2 3
1 2 3 Надо сказать, что некоторые трейдеры и аналитики понимают определение "нормальное" по отношению к распределению слишком буквально. В статистике термин "нормальный" не означает "наиболее часто встречающийся" или "естественный". В XVIII веке математик Кетле проанализировал рост группы солдат и обнаружил (после изображения данных на графике в виде гистограммы), что он нормально распределён. Он решил, что отклонения роста солдат от определённого значения можно объяснить ошибками природы при создании ею "среднего" человека J. Конечно, вполне допустимо считать некоторый параметр, участвующий в расчёте, распределённым по нормальному закону, но следует помнить, что нормальное распределение вовсе не закон природы. Тем не менее большинство инвесторов использует модели, в основе которых лежит предположение о нормальном распределении изменений цен или доходностей, что само по себе является важным фактором, влияющим как на размер, так и на частоту изменений цен (доходностей) рыночных активов (эффект "рефлексивности").
Для того, чтобы грубо оценить степень соответствия фактического распределения изменений рыночной цены определённого финансового актива нормальному распределению достаточно построить в одной системе координат гистограмму фактического распределения частот изменений рыночной цены и кривую нормального распределения с параметрами, соответствующими параметрам фактического распределения. На рисунках ниже сравниваются распределения относительных (доходности) и абсолютных однодневных изменений рыночной цены об.акций РАО ЕЭС (ММВБ) с соответствующими кривыми нормального распределения (глубина исторической выборки 500 дней).
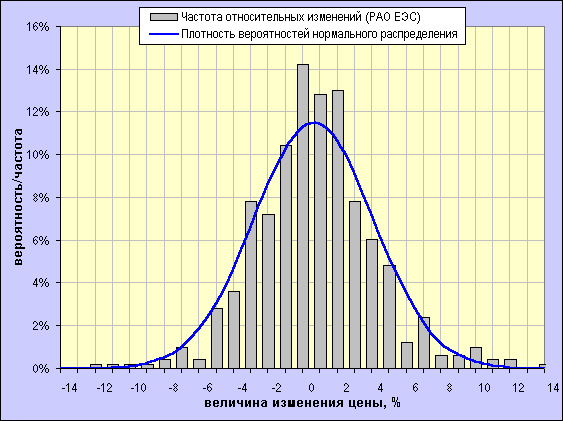
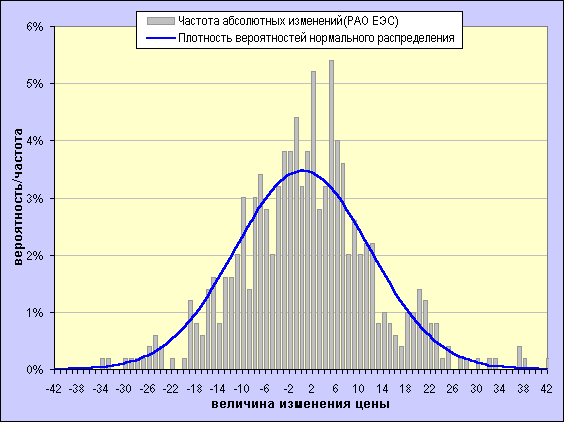
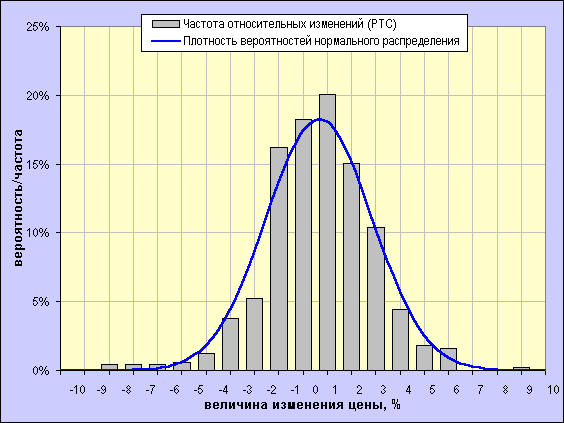
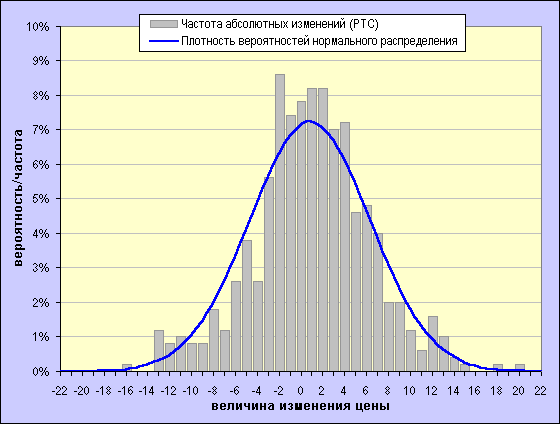
Хорошо заметны отличия фактических распределений от нормального, выражающиеся в более высокой вероятности (частоте) возникновения сравнительно небольших изменений цены и изменений, превосходящих по модулю (иногда весьма значительно) три стандартных отклонения, по сравнению с нормальным распределением. Хочу также обратить внимание на соотношение величин СКО относительных однодневных изменений (доходности) акций РАО ЕЭС (3.47%) и индекса РТС (2.17%) – 1,6, т.е. волатильность (а, значит, и риск) индекса в полтора раза ниже, чем отдельной бумаги, что лишний раз подчёркивает преимущества диверсификации (подробнее читайте в материалах, посвящённых портфельному инвестированию, в разделе "Портфель"). Данные отличия свидетельствуют о не совсем случайном характере изменений цены данного актива и о наличии постоянно или периодически действущих факторов, оказывающих влияние на частоту и величину ценовых изменений. Реальные цены, как мы видим, в целом не так сильно склонны отклоняться от нуля, как это моделируется нормальным распределением, но совершают иногда резкие и сильные скачки (т.е. их распределения имеют т.н. "тяжелые хвосты"). Представленные нормальным распределением случайные изменения с одной стороны, склонны к сравнительно большим колебаниям около нуля, но, с другой стороны, не склонны к резким выбросам. Последнее обстоятельство особенно неприятно, т.к. именно резкие случайные движения цен представляют наибольший "интерес" при оценке возможных потерь. Тем не менее, несмотря на достаточно сильное несоотвествие фактических распределений нормальному и наличие вышеперечисленных недостатков, использование в качестве меры риска дисперсии или СКО ("отрицательной" полудисперсии или полуотклонения) ряда прошлых ценовых изменений является вполне оправданным, т.к. позволяет с определённой степенью достоверности прогнозировать размах будущих колебаний.
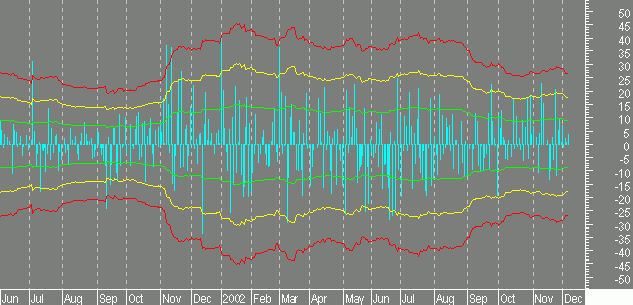
На данном рисунке представлены гистограмма однодневных абсолютных отклонений цены об. акций РАО ЕЭС (в копейках, естественно) и кривые, соответствующие одному (зелёный цвет), двум (жёлтый цвет) и трём (красный цвет) 50-периодным стандатным отклонениям. Обратите внимание, что большинство ценовых изменений по величине не превышает (или незначительно превышает) одно стандартное отклонение, и лишь очень небольшое количество изменений превосходит по величине два СКО. Кстати говоря, одной из причин незначительного и, как правило, однодневного превышения величины СКО может являться практика установки инвесторами "стопов" на данном уровне и периодическое "срывание" их крупными и информированными участниками рынка (т.н. "медвежьи ловушки").
В тех случаях, когда распределение частот изменений цен/доходностей слишком сильно отличается от нормального, более адекватной моделью описания фактических изменений цен/доходности может являться вероятностное распределение, имеющее экспоненциальную форму (распределение Паскаля). Экспоненциальное распределение имеет более выраженный пик (более высокий коэффициент эксцесса) по сравнению с нормальным распределением и более "тяжелые хвосты", что позволяет учесть редкие, но значительные по величине ценовые всплески, вероятность возникновения которых при нормальном распределении, практически, равна нулю. Математически экспоненциальное распределение (строго говоря, распределение Паскаля) определяется следующей функцией плотности вероятностей:
F(x) = e^(-|X| / β) / 2β , где :
X - значение цены (доходности)актива ;
β - среднее абсолютное отклонение, которое для нормального распределения равно:
β = σ / √π/2
σ – стандартное отклонение (СКО).
Ниже приводятся сравнительные графики нормального и экспоненциального распределений применительно к распределению частот относительных однодневных изменений об. акций Ростелекома за 500 дней.
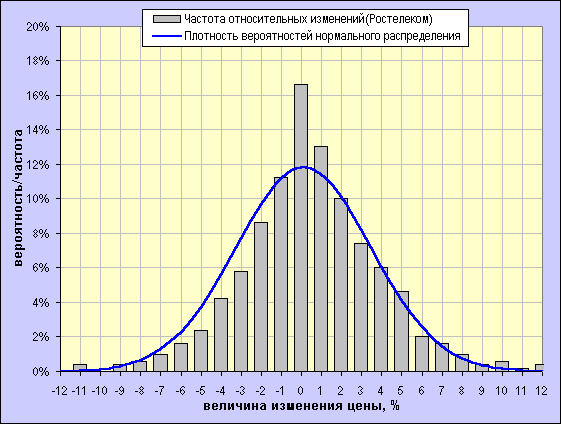
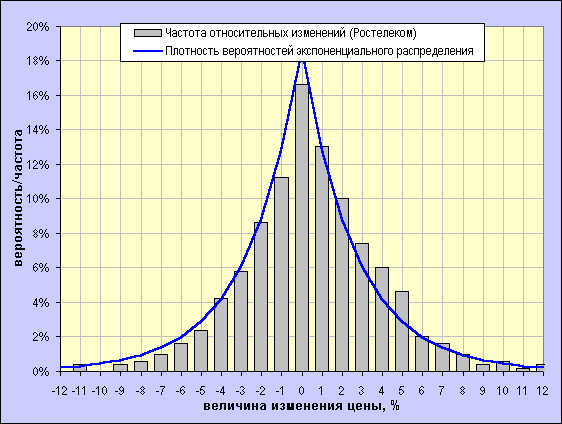
Создаётся впечатление, что экспоненциальное распределение (в данном случае это распределение Паскаля) точнее описывает разброс изменений цен акций Ростелекома, чем распределение Гаусса, что делает его более предпочтительным для моделирования волатильности подобных активов.
Все описанные выше способы измерения исторической волатильности широко распрстранены и крайне просты и легки в вычислении, что, как всегда, имееет и свою обратную сторону в виде следующих недостатков:
В арсенале инвестиционных аналитиков имеются и другие методы расчёта волатильности, в значительной мере лишённые этих недостатков (но, как водится, имеющие свои собственные J ). Применение в качестве меры риска, к примеру, экспоненциальной волатильности позволяет значительно снизить влияние первой группы недостатков, т.к. она (эксп. волатильность) в большей мере отражает недавние изменения цен и не подвержена резким изменениям по факту выхода из выборки достаточно "старых"ценовых выбросов. Экспоненциальная волатильность (не путайте с экспоненциальным распределением! J) отличается от простой тем, что при расчете стандартного отклонения данные исторической выборки включаются в расчёт с весовыми коэффициентами, увеличивающими вес недавних движений цен в выборке по сравнению с давними движениями. Для оценки экспоненциальной волатильности можно использовать следующую формулу*:
Vexp = [(1- SF)*Vexp[1]+ SF*Xi)2]1/2, где :
Xi - значение цены (доходности)актива за i-й интервал ;
Vexp[1] – предыдущее значение волатильности ;
SF – сглаживающий фактор (Smoothing Faxctor, SF) – весовой коэффициент, определяющий степень влияния на волатильность последнего изменения цен по сравнению с более ранними оценками.
* Смотрите также метод расчёта и интерпретацию экспоненциальной скользящей средней в разделе "Акции".
Экспоненциальная волатильность при использовании на практике интерпретируется аналогично простой.
Проблему учета автокорреляции изменений цен (затухающих серий случайных больших ценовых выбросов) финансовых активов при расчете волатильности можно решить с помощью использования ARCH/GARCH-моделей. Процесс авторегрессионной условной гетероскедастичности (ARCH) был впервые разработан Инглом в 1982 году для отражения изменчивости дисперсии во времени. Одно из многочисленных применений этой модели – моделирование волатильности доходности финансовых активов. Рассмотрение особенностей построения и применения ARCH/GARCH-моделей выходит за рамки настоящего материала, но в дальнейшем, возможно, я посвящу этой теме отдельный материал.
В завершение этого краткого обзора статистических методов измерения волатильности хочу обратить внимание на то, что во всех вышеприведённых примерах в качестве переменной распределений использовалось абсолютное либо относительное изменение цен активов. Однако часто трейдеры и аналитики для подобных целей также используют натуральный логарифм отношения цен/доходностей : ln(C t / C t-1). Дело в том, что инвестора, в первую очередь, интересует показатель роста вложенного капитала, т.е. отношение капитала в конечный момент инвестиций к величине капитала в начальный момент. Но инвестиционный процесс состоит, как правило, из серии сделок, каждая из которых имеет в качестве результата определённый коэффициент прироста капитала - C t /Ct-1 , а финансовый результат всей последовательности сделок будет равен произведению этих коффициентов: (C t /Ct-1)* (C t-1 /Ct-2)* (C t-2 /Ct-3)*… (C t-n /Ct0) ; Это может быть выражено суммированием, если использовать натуральные логарифмы отношений цен. Это достаточно привлекательная модель распределения отношений цен ценных бумаг, потому, что, если цена растёт, то отношение цен будет больше единицы, если падает – то отношение цен будет меньше единицы, но никогда не примет отрицательного значения. В свою очередь, если распределение натуральных логарифмов отношений цен подчиняется нормальному закону, то отношения изменений цен будут распределены логнормально. Логнормальное распределение часто используется для моделирования случайных отклонений, в основе которых лежит процесс умножения.